Leetcode 212. 单词搜索II

Author: Carissa ⛽️

Date: Dec.28 2023 😈

Link: 212. 单词搜索 II - 力扣（LeetCode）

1 题目

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words， 返回所有二维网格上的单词 。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

提示：

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 10^4
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同

示例 1：

输入： board = [[“o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”]], words = [“oath”,”pea”,”eat”,”rain”]

输出： [“eat”,”oath”]

示例2:

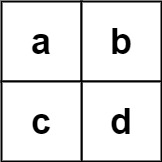
输入： board = [[“a”,”b”],[“c”,”d”]], words = [“abcb”]

输出： []

2 思路

2.1 暴力解法

2.1.1 最暴力的解法

在做本题时我首先使用了遍历 words 中所有单词，对每个单词 word，从 board 的 [0,0] 处开始，如有匹配则做 dfs。这种解法，理所当然地，超时了。

时间复杂度是：$O(m\times n \times 4^l)\times O(\sum_{i=0}^{words.length}wrods[i].length)$

空间复杂度是：$O(1)$

m == board.length, n == board[i].length, l是所有单词的平均长度

2.1.2 暴力但是情有可原的解法

转换思路，还有一种暴力解法，先将所有 word 放入哈希表中，遍历 board 中的每一个字符，以每一个字符作为起始点dfs搜索，看是否有以该字符为开头的单词在哈希表中。为什么这个方法可行呢？因为题目中明确规定了 1 <= words[i].length <= 10, 即单词长度不超过 10。

这就意味着，dfs 的退出条件是找到单词，或者搜索深度大于10。

这种思路里，用 StringBuffer 或 StringBuilder 的长度记录搜索深度，当然本题用 ==StringBuffer 会超时😊==。

时间复杂度：$O(m\times n \times 4^{10})$

空间复杂度：$O(\sum_{i=0}^{words.length}wrods[i].length)$

2.2 Trie + 搜索

再对 2.1.2 做优化，结合单词，可以想到的就是 Trie 前缀树

这次做前缀树发现一个小技巧 👀：

💡 可以不用 boolean isEnd 作为结尾标记，而是采用 String value 只在单词结尾存入整个单词的方法做标记。这样在搜索过程中也不需要 StringBuilder 来额外记录当前搜索字符了。

3 复杂度分析

时间复杂度：

$O(m\times n \times 4^{10})$

空间复杂度：

$O(\sum_{i=0}^{words.length}wrods[i].length \times C)$

$C：$字符集大小，固定为26

4 完整解法

class Solution{
    class TrieNode {
        String word;
        TrieNode[] childrens = new TrieNode[26];
    }
    void insert(String word) {
        TrieNode p = root;
        for(int i = 0; i < word.length(); i++) {
            char ch = word.charAt(i);
            int index = ch - 'a';
            if(p.childrens[index] == null){
                p.childrens[index] = new TrieNode();
            }
            p = p.childrens[index];
        }
        p.word = word;
    }

    Set<String> set = new HashSet<>();
    List<String> ans = new ArrayList<>();
    char[][] board;
    int m, n;
    TrieNode root = new TrieNode();
    int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    boolean[][] vis = new boolean[15][15];
    public List<String> findWords(char[][] _board, String[] words) {
        board = _board;
        m = board.length; n = board[0].length;
        for(String w : words) insert(w);
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                int u = board[i][j] - 'a';
                if(root.childrens[u] != null) {
                    vis[i][j] = true;
                    dfs(i, j, root.childrens[u]);
                    vis[i][j] = false;
                }
            }
        }
        for(String s : set) {
            ans.add(s);
        }
        return ans;
    }

    void dfs(int i, int j, TrieNode node) {
        if(node.word != null) set.add(node.word);
        for(int[] d:dirs) {
            int r = d[0] + i, c = d[1] + j;
            if(r < 0 || r >= m || c < 0 || c >= n || vis[r][c]) continue;
            int u = board[r][c] - 'a';
            if(node.childrens[u] != null) {
                vis[r][c] = true;
                dfs(r, c, node.childrens[u]);
                vis[r][c] = false;
            }
        }
        
    }
}